Using an Anemometer
How to Use an Anemometer to Make Mass Flow Rate Measurements
An Emprise Anemometer measures air velocity. We calibrate Anemometers such that the blade speed in revolutions per second can be converted into air velocity in feet per second using a linear best fit equation.
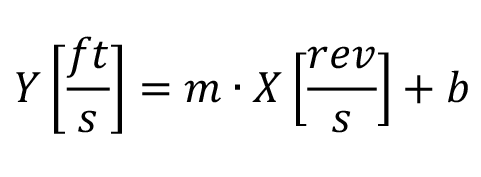
Where “Y” is the air velocity, “m” is the slope, “X” is the blade speed, and “b” is the intercept. The calibration constants are marked in Yellow at the bottom of the calibration sheet.
The blade speed is not the frequency. To convert from frequency to blade speed, divide the frequency by the number of “ticks” per revolution. We produce several different blade configurations. To determine the number of ticks on our “flag type” blade, simply count the number of blades. The flag is the parallelogram shaped blade tip. On our “solid ring type”, the blades are joined at the outer circumference by an encoder ring. The number of “ticks” is the number of holes in the ring.
Our calibration wind tunnel provides free-field flow in the test section. That means that the air speed is uniform across the area of the anemometer blades. Our calibration is not valid for fully-developed flow. Air flow in a duct has a parabolic velocity profile across the diameter of the duct. The air velocity at the wall of the duct is zero and increases toward the center of the duct. When using our anemometer in a duct that is the same or nearly the same diameter, the velocity across the instrument will not be uniform and accuracy will suffer. To maintain accuracy when using the anemometer to measure air speed in a duct, we recommend calibrating the anemometer for the specific application.
An anemometer is not a mass flow meter by itself; but, by adding a static pressure transducer and temperature measurement, the mass flow can be calculated using the following equations.
The Ideal Gas law
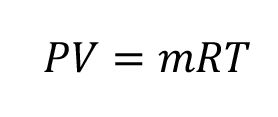
Where “P” is the absolute static pressure measured near the anemometer in, ; typically measured at the duct wall. “V” is the volume in, ; “m” is the mass in, ; “R” is the Universal Gas Constant, which for air is, ; and “T” is the temperature at the anemometer in degrees Rankine. With a little algebra, this equation renders the Air Density:
Mass flow rate
Where “” is the mass flow rate in, ; “” is the density calculated from the equation above; “A” is the unblocked cross-sectional area at the anemometer; and “V” is the air velocity reported by the anemometer. The anemometer blockage is included on the calibration sheet. The unblocked area is the total cross-sectional area at the Anemometer minus the blockage due to the anemometer and any mounting hardware.
Now that we have all the equations, just collect the data from the pressure transducer, temperature sensor, and the Anemometer. Add the following equation to your data collection software or data log spreadsheet for the mass flow rate:
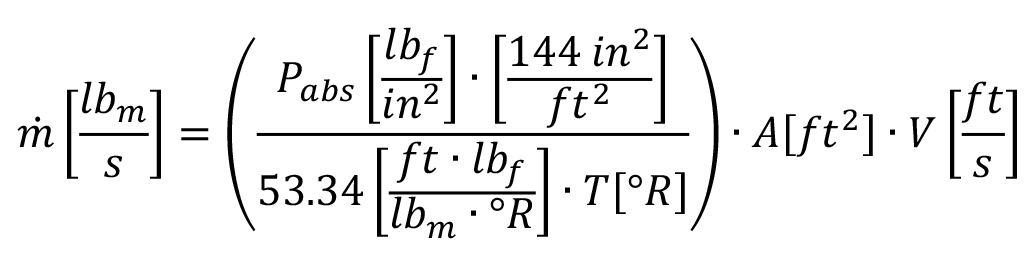
This can be simplified to

When calculating the Mass Flow Rate, make sure to use the engineering units, shown in the equation above. Once derived, convert the result from, to any engineering units you need.